- 논문 제목: mHC: Manifold-Constrained Hyper-Connections (mHC: 다양체 제약이 있는 하이퍼 연결)
- 저자: Zhenda Xie, Yixuan Wei, Huanqi Cao 외 (DeepSeek-AI 팀)
- 게재 정보: arXiv:2512.24880
- 발표 연도: 2026년 1월
- 논문 링크: https://arxiv.org/pdf/2512.24880
Summary
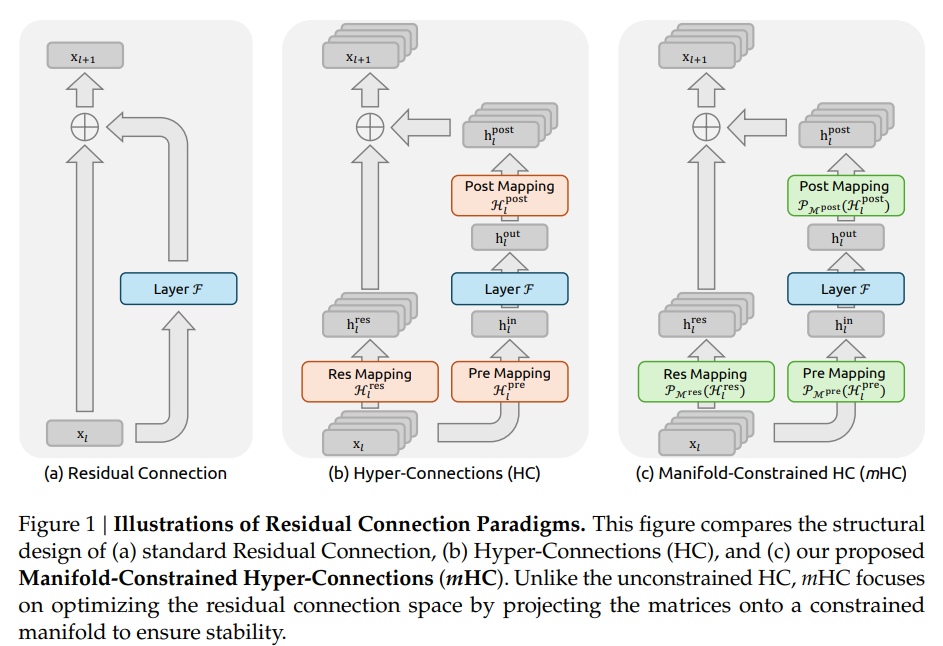
Micro design은 사실 모두가 달려들어서 MLA, Deepseek Sparse Attention 같은거 하다 보니깐 많이 발전 했었는데, Macro design으로써 여기저기 쓰이는 residual connection 보면, 사실 resnet 에서의 아이디어와 크게 다름이 없다.
사실 residual connection이 너무 심플해서, 이걸 개선한다는게 어려워보이는 부분이긴 하다. 기존에 HC라는 연구가 있었는데, 이는 residual connection의 채널수를 높이고, 마치 H를 게이팅처럼 작동하게 해서 잔차 연결의 Capacity를 높이는게 목적이였다.
하지만 HC는 학습이 불안정한 문제가 있었고, mHC는 를 manifold에 투영해서 해결한다.
Preliminary
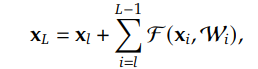
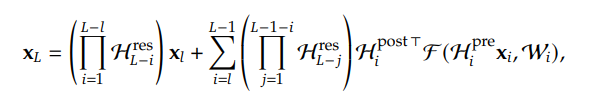
근데 아쉽게도 위 식을 보면 알겠지만, HC로 계속해서 연결을 하다보면 행렬곱이 계속해서 나오는 형태가 나오고, HC에서는 이 부분이 발산하지 않게 해주는 어떠한 보장도 해주지 않는다.
Method
여기서 mHC의 핵심이 나온다. mHC는 Sinkhorn-Knopp 알고리즘을 통해서 를 doubly stochastic matrix로 만들고, 이는 아무리 곱해도 doubly stochastic matrix이므로 곱셈에 닫혀있다. doubly stochastic matrix들의 집합으로 만들어진 manifold를 Birkhoff Polytope라고 부른다고 한다. 그러므로 논문 제목의 manifold는 Birkhoff Polytope을 말하는것.

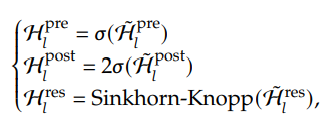
Experiments
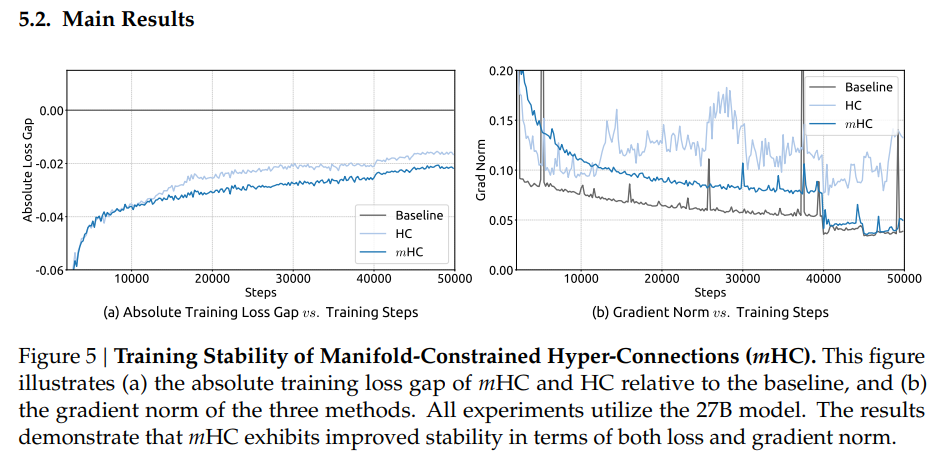
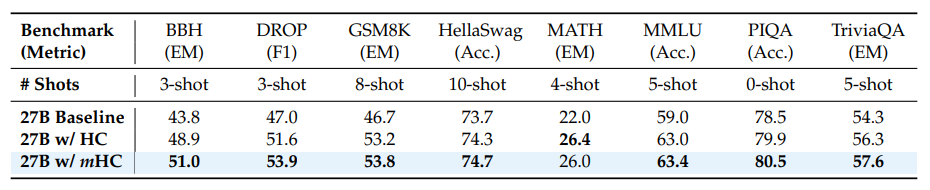
HC랑 다르게 학습이 잘 되고, 27B같이 큰 모델에서도 잘 학습이 된걸 볼 수 있다.
Conclusion
매크로적 연구가 확실히 마이크로 구조 연구보다는 적은것 같다. 딥시크 연구진들은 이것에 대해서 사람들이 더 많이 관심을 가져야 할 것 같다고 말하면서 논문은 끝난다.
수학도 지적유희적으로 사용된게 아니라 정확한 논리를 위해서 합리적으로 사용되었고, 학습은 아주 큰 모델에 직접 학습을 해서 보여줬다. 사람들이 좋아하는 논문의 두가지를 다 충족하는것 같다.
나중에 한번 더 자세히 볼 가치가 있을 것 같은 논문인것 같다.